Numbers drive everything from simple counting to complex calculations. Although most of them are conjecturable, there are those that contain indefinite mysteries. This basic mathematical difference opens the door to an improved understanding of all of computer algorithms to financial calculations.
You are a student, a professional, or a curious learner; the art of mastering this concept gives a firmer basis in all the reasoning numbers.
In this blog, what you’ll discover:
- Foundational Concepts: Clear definitions of rational and irrational numbers with real-world examples
- Rational vs Irrational: Learn to know instantly the difference between the two by a few simple rules and by looking at them.
- Practical Applications: What does this knowledge have to do with technology, engineering, and solving real-life problems?
Let’s get started.
What Are Rational Numbers? The Predictable Performers
The Clear-Cut Definition
Rational numbers are the numbers you can express as a fine fraction so that the numerator (top number) and the denominator (bottom number) are whole numbers and the denominator is not zero.
Mathematical Form: p/q where p, q are integers and q ≠ 0
Simple Translation: If you can express it exactly as a fraction or ratio, it’s rational
Everyday Examples You Already Know
Simple Fractions: ½, ¾, -2/5
Whole Numbers: 5 (which equals 5/1), -12 (as -12/1)
Zero: 0 (as 0/1, 0/2, etc.)
Repeating Decimals: 0.333… (which equals 1/3)
Their Reliable Properties
Rational numbers follow predictable rules that make them easy to work with:
- Closure: Adding, subtracting, or multiplying any two rational numbers always gives another rational number
- Commutative Nature: 2/3 + 1/4 = 1/4 + 2/3 (order doesn’t matter)
- Associative Property: (1/2 + 1/3) + 1/4 = 1/2 + (1/3 + 1/4)
- Identity Elements:
- Additive: 2/3 + 0 = 2/3
- Multiplicative: 2/3 × 1 = 2/3
Types of Rational Number
Positive Rationals: Numbers greater than zero (3/4, 5/1, 2.5)
Negative Rationals: Numbers less than zero (-2/3, -7, -1.25)
Special Case – Zero: The neutral member that’s neither positive nor negative
What Are Irrational Numbers? The Mathematical Rebels
The Definition That Defies Fractions
The mathematical mysteries are irrational numbers, which cannot be presented as simple fractions of numbers. Their decimal expansions are infinite in nature, and never reach a repetitive cycle.
- Mathematical Reality: Cannot be written as p/q where p and q are integers
- Decimal Behavior: Non-terminating and non-repeating decimal expansions
- Simple Truth: If you can’t write it as a clean fraction, it’s likely irrational
Famous Examples You’ve Actually Used
- Mathematical Constants:
- π (pi) ≈ 3.1415926535…
- e (Euler’s number) ≈ 2.7182818284…
- φ (golden ratio) ≈ 1.6180339887…
- Radical Realities:
- √2 ≈ 1.4142135623…
- √3 ≈ 1.7320508075…
- √5 ≈ 2.2360679774…
Properties of Irrational Numbers
Irrational numbers behave differently from their rational counterparts:
- Infinite Decimals: They have a continuously growing process of the number of digits and do not repeat.
- Fraction Resistance: You can not make them as fractions, however hard you may struggle to do it.
- Density of Number lines: There exist irrationals between any two rational numbers.
- Operation Quirks:
- The rational and irrational numbers always add to the irrational number.
- Multiplying a non-zero rational by an irrational number stays irrational
Key Difference Between Rational and Irrational Numbers
Understanding the distinction between these number types is simpler when you focus on their fundamental behaviors and representations.
The Detailed Comparison Table
Feature | Rational Numbers | Irrational Numbers | Why This Matters |
Representation | When p and q are integers, it can be expressed as p/q. *Example: 3/4, -2/1* | Cannot be represented as one integer divided by another. Example: √2, π | Determines how easily we can work with them in calculations |
Decimal Form | Terminating (0.5) or repeating (0.333…) Pattern eventually repeats | Non-terminating, non-repeating No pattern ever emerges | Affects precision in measurements and computing |
Common Examples | 2/3, -5, 0.75, 7 Tidy, predictable values | √2, π, e, √5 Mathematical mysteries | Shows where each type appears in real applications |
Countability | Countable – can be listed in sequence Like pages in a book | Uncountable – cannot be comprehensively listed Like grains of sand |
Rational Irrational Numbers Chart
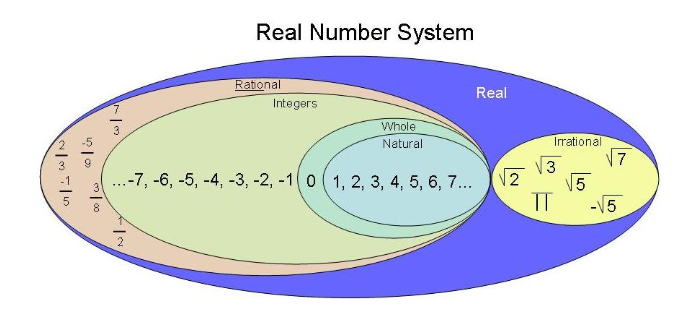
How to Identify Rational and Irrational Numbers
Think of yourself as a number detective. With these simple investigative techniques, you can quickly classify any number you encounter.
The Step-by-Step Identification Method
Step 1: The Fraction Test
- Try to express the number as a fraction of two integers
- Rational clue: 0.75 = 3/4 ✓
- Irrational clue: π ≠ any integer fraction ✗
Step 2: The Decimal Examination
- Look at the decimal expansion carefully
- Rational pattern: 0.1666… (repeating) ✓
- Irrational pattern: 1.414213562… (no repetition) ✗
Step 3: The Root Investigation
- Check if it’s a square root of a non-perfect square
- Rational case: √16 = 4 ✓
- Irrational case: √2 ≈ 1.4142135623… ✗
Case Study: Why √2 is Irrational
The ancient proof is elegant:
- Assume √2 is rational: √2 = a/b (where a,b are reduced)
- Then 2 = a²/b² → a² = 2b²
- This means a² is even, so a must be even
- If a is even, then b must be odd to keep a/b reduced
- But if a is even, then a² is divisible by 4, making b² even
- Contradiction! Therefore, √2 cannot be rational
The Decimal Detective’s Quick Guide
- Terminating decimal (0.25) → Definitely rational
- Repeating pattern (0.333…, 0.142857142857…) → Definitely rational
- No pattern, goes forever (1.010010001…) → Definitely irrational
Pro Tip: When you see famous constants like π or e, remember they’re the celebrities of the irrational number world – they never settle into repeating patterns!
Real Numbers and Their Classification
Understanding where rational and irrational numbers fit in the mathematical universe helps you see the beautiful organization behind all numbers.
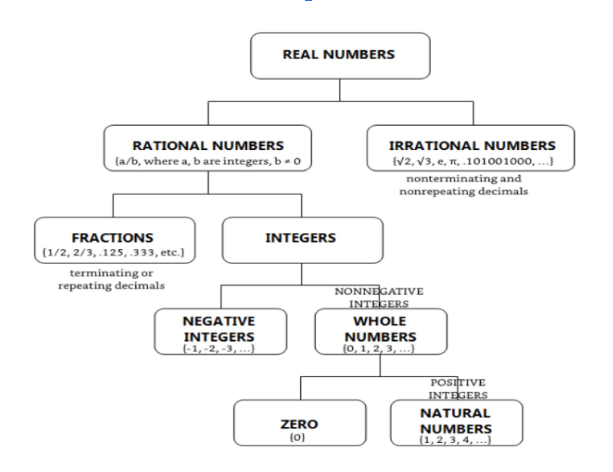
Key Relationships to Remember
- Mutual Exclusivity: A number can be rational OR irrational—never both
- Complete Coverage: It is a combination of rational and irrational numbers that constitute ALL real numbers.
- Number Line Density: Between any two rational numbers, you’ll find infinitely many irrational numbers, and vice versa
Why This Classification Matters
In computer science and IT, this hierarchy explains:
- Why floating-point arithmetic has precision limits (handling irrationals)
- The way the different types of data are constructed to accommodate the various types of numbers.
- The reason why certain computations are precise and some have to be approximate.
Real-Life Examples of Rational and Irrational Numbers
You encounter both rational and irrational numbers daily, often without realizing it. Let’s explore where these mathematical concepts appear in our everyday world.
Rational Numbers in Daily Life
These predictable numbers help us measure, divide, and calculate with precision:
- Cooking & Recipes: ½ cup flour, ¾ teaspoon salt
- Financial Transactions: $3.50 coffee, 25% discount
- Construction: 0.75 meter plank, ⅝ inch pipe
- Time Management: 15 minutes (¼ hour), 45 minutes (¾ hour)
Why They Work: Their exact fractions and terminating decimals make them perfect for measurements where precision matters.
Irrational Numbers in the Real World
These mathematical constants appear in nature, engineering, and design:
- Circle Calculations:
- Wheel circumference = π × diameter
- Pizza area = π × radius²
- Geometry in Design:
- Square table diagonal = side × √2
- Golden ratio φ in art and architecture (≈1.618)
- Advanced Applications:
- Compound interest calculations using e
- Signal processing with trigonometric functions
The Pattern: Irrational numbers often emerge in continuous, natural phenomena and perfect geometric relationships.
Quick Reference Guide
Scenario | Number Type | Why It Appears |
Measuring ingredients | Rational | Exact fractions needed for recipes |
Calculating screen size | Irrational | Diagonal measurement involves √2 |
Building circular structures | Irrational | π relates circumference to diameter |
Financial percentages | Rational | Exact decimals for precise calculations |
Remember: While we approximate irrational numbers in daily use (π ≈ 3.14), their true values continue infinitely without repetition, revealing the beautiful complexity of our mathematical universe.
At a Glance: Rational vs. Irrational Numbers
Here’s your quick-reference guide to these fundamental number types—perfect for students, professionals, and anyone looking to solidify their math fundamentals.
Quick-Reference Comparison Table
Feature | Rational Numbers | Irrational Numbers |
Basic Definition | Can be written as a fraction p/q where p and q are integers | Cannot be expressed as an exact fraction of integers. |
Decimal Form | Terminating (0.5) or repeating (0.333…) | Non-terminating, non-repeating (3.1415926535…) |
Everyday Examples | 1/2 (recipe measurement), 0.25 (quarter dollar), -3 (temperature) | π (circle calculations), √2 (diagonal measurements), e (growth models) |
Mathematical Examples | 5/1, -2/3, 0.75, 7, 0.1666… | √3, √5, π, e, φ (golden ratio) |
Number Line Behavior | Can be plotted exactly at specific points | Fill in the gaps between rational numbers |
Mathematical Properties | Closed under +, -, × operations | Not closed under basic operations |
Computational Handling | Can be represented exactly in calculations | Require approximation in computing |
Pro Tip: How to know what type of number to use as fast as possible? Try writing it as a fraction. It is logical in case you can succeed with integers. Otherwise-and the decimals of numbers are never repeated-you have an irrational number.
This sharp differentiation can be of immense importance in computer science and engineering, and data analysis, where knowledge of number behavior influences all aspects of algorithm design as well as the accuracy of measurement.
Conclusion
Understanding the obvious distinction between rational and irrational numbers offers a heuristic perspective on making sense of the logic of mathematics as such. Rational numbers with their clean fractions and repeatable decimals provide us with precision and predictability in areas such as finance and software engineering.
In the meantime, irrational numbers, such as 1.57 and 1.414 – the decimals of 1.57 and 1.414 are both infinite and non-repeating- 2 demonstrate the complexity and the not-finite nature of our world, whether in the circular arts or in the geometric growth.
This is beyond theoretical knowledge; it is an actual tool that will help us to be more numerically literate so that we make better choices in technology, science, and life in general. Through understanding this fundamental concept, you would have a better basis for all mathematical reasoning in the future.
