When you look outside to see the temperature, when you measure the ingredients you need to make a recipe, and when you look at your bank account, you are working with real numbers. It is these values that create the fundamental base of the daily math and the daily computation. Essentially from simple addition all the way to elaborate algorithms, real numbers give the mathematical backbone on which simple arithmetic and complex computer systems are run. We will find out what is so basic about these numbers as far as mathematics and technology is concerned.
What Exactly Are Real Numbers?
Now, we will deconstruct this basic concept of math that you apply in your everyday life, even without noticing.
The Formal Definition
The expression of all real numbers is denoted by mathematicians by the symbol ℝ. Method: In this method, one considers the totality of numbers that can be placed in a number line – no holes, no gaps. This family includes:
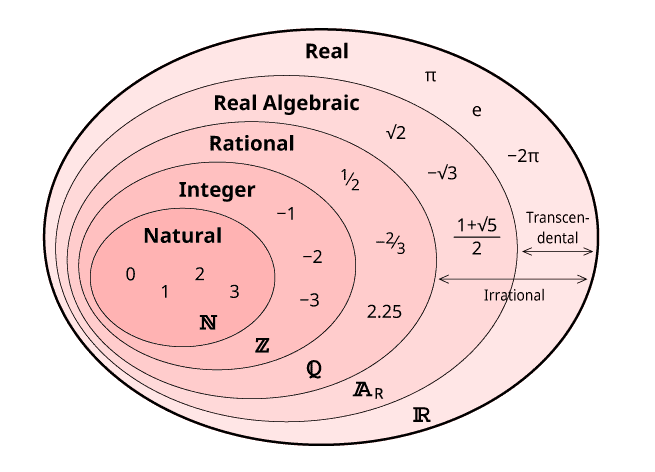
Two Main Categories:
Rational Numbers: These behave nicely – think fractions (¾), whole numbers (-2, 0, 5), and decimals that end or repeat (0.75, 0.333…)
Irrational Numbers: The rebels that never repeat – like π (3.14159…) and √2 (1.41421…)
Practical Examples:
- The 72.3°F temperature showing on your thermostat
- The $4.65 charge for your morning coffee
- The 4.25-inch screen on your smartphone
- The -15°C reading on your weather app
Types of Real Numbers
Think of real numbers as a family tree, with each type representing a different generation or branch. Let’s meet the key members of this mathematical family.
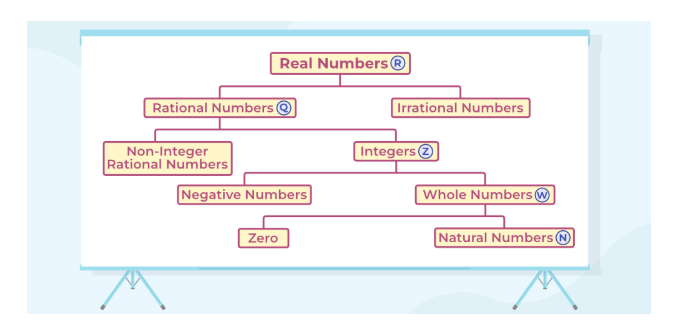
- Natural Numbers (N)
- What they are: The counting numbers we learn as children
- Examples: 1, 2, 3, 4, 5… (and so on forever)
- Real-world use: Counting discrete objects – 3 apples, 15 students, 100 pages
- Whole Numbers (W)
- What they are: Natural numbers plus zero
- Examples: 0, 1, 2, 3, 4…
- Real-world use: Representing nothing or absence – 0 dollars, 0 customers, 0 errors
- Integers (Z)
- What they are: Whole numbers plus their negatives
- Examples: …-3, -2, -1, 0, 1, 2, 3…
- Real-world use: Tracking gains/losses – -$250, -5°C, +10 points
- Rational Numbers (Q)
- What they are: Numbers expressible as fractions
- Examples: ½, 0.75, -2.5, 3 (which is 3/1), 0.333…
- Real-world use: Precise measurements – ¾ cup flour, 2.5 miles, 25% discount
- Irrational Numbers (I)
- What they are: Numbers that cannot be written as fractions
- Examples: π (pi), √2, e (Euler’s number)
- Real-world use: Exact mathematical constants – circle calculations (π), diagonal measurements (√2)
Properties of Real Numbers
Understanding these fundamental properties of real numbers is like learning the rules of the road for mathematics. They govern how numbers behave in operations and form the foundation for algebra and beyond.
- Closure Property
- Concept: Performing operations on real numbers keeps you in the real number family
- Example: 5 + 7 = 12 (both addition and result are real numbers)
- Commutative Property
- Concept: You can swap numbers in addition/multiplication
- Addition: 8 + 3 = 3 + 8
- Multiplication: 4 × 6 = 6 × 4
- Associative Property
- Concept: Grouping doesn’t affect addition/multiplication results
- Addition: (2 + 5) + 1 = 2 + (5 + 1)
- Multiplication: (3 × 4) × 2 = 3 × (4 × 2)
- Distributive Property
- Concept: Multiplication distributes over addition
- Example: 3 × (4 + 2) = (3 × 4) + (3 × 2)
- Identity Property
- Additive Identity: Adding zero changes nothing → 9 + 0 = 9
- Multiplicative Identity: Multiplying by 1 changes nothing → 7 × 1 = 7
- Inverse Property
- Additive Inverse: Number + its opposite = 0 → 6 + (-6) = 0
- Multiplicative Inverse: Number × its reciprocal = 1 → 2 × (½) = 1
These properties of real numbers create the consistent, predictable system that makes everything from simple arithmetic to complex programming possible. They’re the invisible rules that keep mathematics reliable and universal.
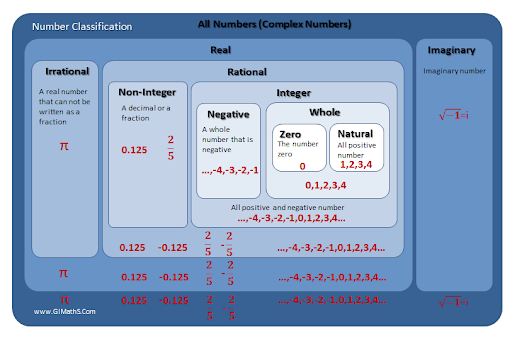
What Numbers Aren’t Considered Real?
By real numbers, we mean the entire line of continuous numbers. But there are mathematical ideas that do not fit in this line. We should take a look at what is beyond the real numbers.
Imaginary Numbers: Solving the Impossible
Consider trying to locate a number that, when multiplied by itself, gives out a negative number. This seemed to be impossible for mathematicians for centuries. Then they came up with imaginary numbers.
The imaginary unit is i, which is the square root of negative one. This means:
- √-4 becomes 2i
- √-9 becomes 3i
- √-1 is simply i
These numbers don’t exist on our traditional number line. On the contrary, they develop an entirely new dimension of numbers. Combining real numbers and the imaginary numbers (3 + 2i), you obtain what mathematicians term complex numbers.
When Math Breaks: Undefined Operations
Certain mathematical operations do not form valid numbers. The most notorious one is division by 0.
Consider it: In your attempts at the division of 10/0, you are really asking: how many times did 0 multiply by it, 10? There is no such number. That is why the calculators render a value of undefined error.
Similarly, division of 0 by 0 is a special problem known as indeterminate; it is possible in theory to be any number, thus mathematically useless.
Real vs. Imaginary: A Practical Difference
Although imaginary numbers may sound like a piece of abstract nonsense, they are incredibly useful in the real world. Electrical engineers employ them to study AC circuits, physicists to study quantum mechanics and they are a necessity in signal processing of everything between a radio and a smartphone.
Therefore, these numbers are not real in the mathematical sense of the word, but are very very real in their practice. The major difference is that the real numbers are the measurable and continuous number, whereas imaginary numbers are the solution to the problem which cannot be solved using the real number.
How Real Numbers Fill the Number Line
Imagine a straight line that runs all the way and extends to the bare ends. This is the actual line – a continuous unbroken line, in which each single point is specifically associated with an exact real number, and in which each real number has its own position.
The Continuous Nature
The actual number line is solid compared to a dotted line where one may notice gaps. When you have two numbers of any kind you want to study that are separated by even the closest distance, there is still another number, just waiting to be discovered. The smooth sample enables the real numbers to be ideal in the measurement of continuous quantities such as distance, time and temperature.
How Different Numbers Fill the Line
Feature | Rational Numbers | Irrational Numbers |
Role | Create a dense, predictable pattern | Act as the “missing pieces” |
Definition | Numbers that can be expressed as a fraction of two integers (e.g., ½, -7). Their decimal form terminates or repeats. | Numbers that cannot be expressed as a fraction. Their decimal form is infinite and non-repeating. |
Examples | ½ (0.5), ⅓ (0.333…), -2.75 | π (3.14159…), √2 (1.41421…), e (2.71828…) |
How They Fill the Line | They are so densely packed that between any two, you can always find another. However, they still leave infinitesimal gaps. | They perfectly fill the microscopic gaps left between the rational numbers, creating a truly continuous and unbroken line. |
Real Numbers in Everyday Life
You may have assumed that real numbers are purely some abstract concept that exists in mathematics yet you actually use them on a daily basis. These figures are our daily invisibles: to look up the time to keep track of your budget.
In Measurements and Quantities
Every measurement you take relies on real numbers:
- Cooking: Following a recipe for 2.5 cups of flour or 0.75 tsp of salt
- Shopping: Calculating that 3.5 pounds of apples at $1.29 per pound
- Travel: Charting that you have travelled 15.7 miles with the speed of 42.5 miles per hour.
- Weather Checking outside it is 72.3 o F and humidity is 30%.
In Banking and Finance
Your financial life runs on real numbers:
- Interest Rates: Earning 2.25% APY on your savings account
- Loan Payments: Paying $347.85 monthly on your car loan
- Investments: Watching your portfolio grow by 5.7% this quarter
- Budgeting: Allocating 30% of your income to housing costs
In Engineering and Construction
Behind every structure and device are precise real numbers:
- Architecture: Calculating that a beam must support 1,250.75 pounds
- Electronics: Designing circuits with 12.6 volts and 2.2 amps
- Manufacturing: Cutting materials to within 0.001 inch tolerance
- Software: Processing decimal values in financial and scientific applications
Conclusion
Your journey with real numbers is just beginning. This basic system of numbers is the portal to a larger part of higher mathematics:
- Algebra is based on properties of real numbers in solving equations.
- Calculus depends on the continuous nature of real numbers to handle limits and derivatives
- Computer Science uses real numbers in algorithms and data processing
- All engineering uses real numbers to create manufactures anything ranging to microchips to bridges.
Every time you take measurements of the ingredients, take a check of the bank account or calculate the time to travel, you are working with the same real numbers that drive the greatest social scientific research and technological innovation. Learning this concept will not only be valuable in math class- this is the numerical language of our universe that one learns.
FAQs
What are real numbers with examples?
The real number consists of all rational and irrational numbers, which may be found in a number line. Some examples are whole numbers (5), fractions (0.75), decimals (2.75) and irrationals such as 1/2 (pi) and the square root of 2 ( sqrt2 ).
What is not a real number?
The number √-1 (imaginary because it is represented by the square root of a negative number) i and the division by zero are not real numbers. They exist beyond the continuous number line which constitutes real numbers.
Are all integers real numbers?
Yes, absolutely. Integers (…-2, -1, 0, 1, 2,… ) are a sub-set of real numbers. These are the whole numbers and their negations which come at regular intervals on the number line.
What is the difference between rational and real numbers?
Fractions of integers are called rational numbers and it has rational numbers as well as irrational numbers (such as π and 2) which cannot be called fractions.
Why are real numbers important in mathematics?
Algebra, calculus, and higher mathematics are based on real numbers since real numbers generate a continuous number line with no gaps. This will result in accurate measurements and easy mathematical procedures.
What are the 7 properties of real numbers?
The most important ones are addition, multiplication, associative, distributive, inverse (additive and multiplicative), identity, and commutative. These laws control the behaviour of real numbers in all the mathematical operations.
